Michael Lindsey

Background. For many intractable optimization problems, it is possible to formulate a convex relaxation by making use of simple structure in the objective function. Examples range from combinatorial optimization problems (such as the famous Max-Cut problem) to the problem of determining the ground state energy of a quantum many-body system, which is of fundamental importances in quantum chemistry and condensed matter physics. Relaxations are derived by writing down necessary constraints satisfied by some reduced variable in the original problem. Often the resulting problem has the structure of a semidefinite program (e.g., the Goemans-Williamson algorithm for Max-Cut and the 2-RDM theories of quantum chemistry).

Quantum marginals. We have introduced a new type of 'quantum marginal' relaxation for quantum many-body problems and developed a scalable solver for it. This relaxation carries the interpretation of a quantum embedding theory (see Quantum embedding below), which motivates the solver.

Classical marginals. The aforementioned 'quantum marginal' relaxation extends preceding work on a classical marginal relaxation for discrete multi-marginal optimal transport problems. With a multiscale approach, we have extended this classical marginal relaxation to solve general continuous global optimization problems with pairwise structure, which include sensor network localization and optimal molecular configuration problems.

General semidefinite programming. More broadly I am interested in optimization for general SDP, particularly with low-rank structure.

Pictured: A partition of a lattice system into disjoint fragments.

Background. The fundamental difficulty of quantum many-body problems is that the complexity of the quantum wavefunction grows exponentially with the number of particles in the system. Recently, quantum embedding theories have made progress in addressing this difficulty by dividing systems into smaller fragments, which can themselves be treated with an accurate 'high-level' theory, perhaps even implemented on a quantum computer! These local problems are coupled together self-consistently via some coarse global physical quantities.

Variational embedding. Our recently introduced variational embedding theory is the first embedding theory which provides a guaranteed bound on the ground-state energy. However, in its original formulation as an abstract semidefinite program, the theory is hard to solve numerically. By making use of quantum embedding intuition, we have introduced a scalable solver for this semidefinite program. This approach solves effective 'high-level' local problems in parallel, where the effective problems are determined self-consistently by updates that enforce coarse global constraints.

Other embedding methods. I have also worked on improving the scaling and robustness of existing quantum embedding theories, including density matrix embedding theory (DMET) and dynamical mean-field theory (DMFT). I am also interested in improving the mathematical understanding of impurity problems, which are the embedded subproblems in DMFT, as well as DMFT itself.

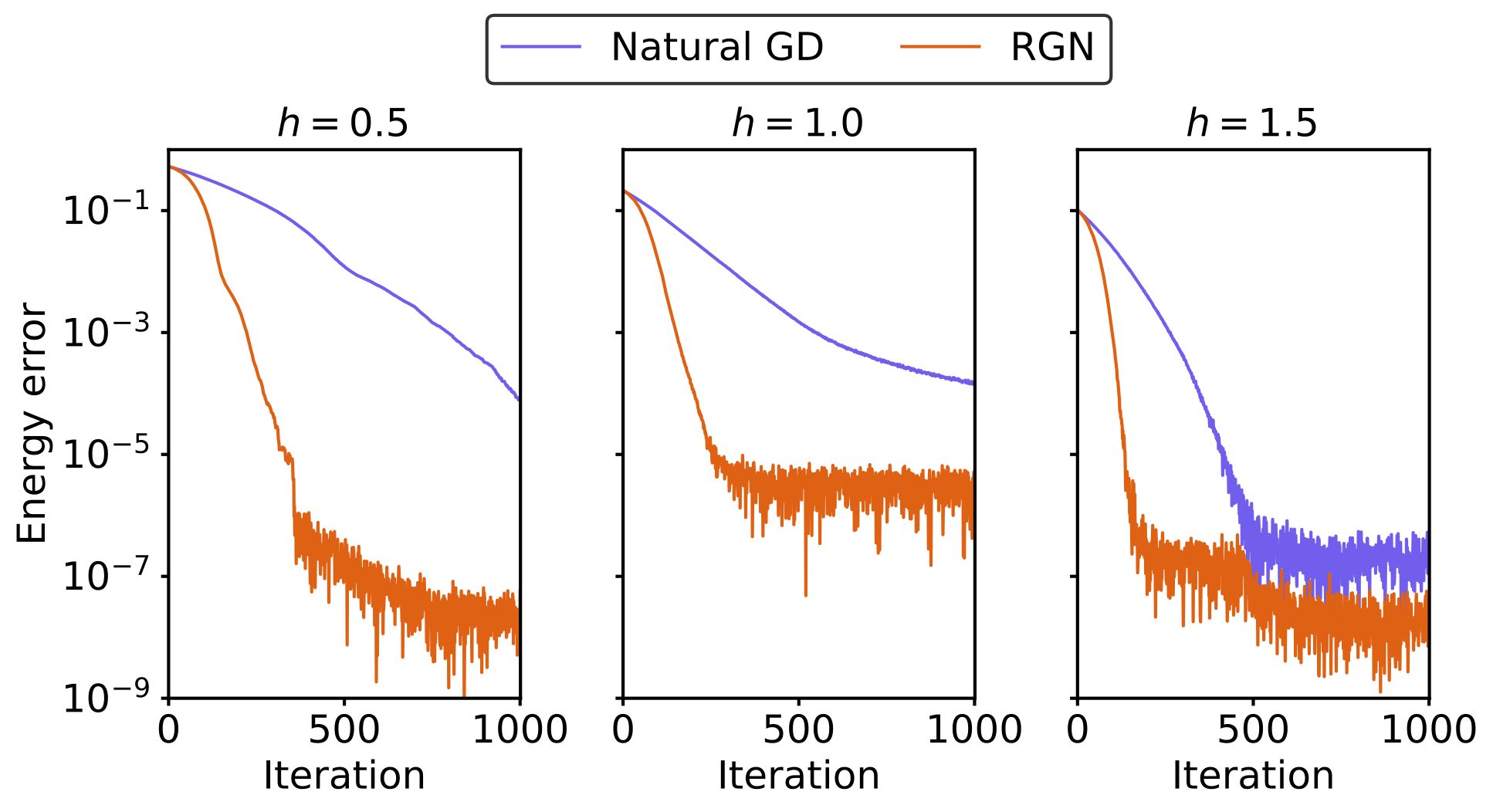Pictured: The Rayleigh-Gauss-Newton (RGN) method exhibits fast convergence for the 1D transverse-field Ising model, maintained through the quantum phase transition at h=1.

Background. Many scientific computing problems can be viewed as optimization problems over functions on high-dimensional state spaces (discrete or continuous). Such problems include the ground-state eigenvalue problem for quantum many-body problems, as well as the problem of computing committor functions to characterize reaction pathways in computational chemistry. A well-chosen parametric class of functions (such as a tensor network or neural network parametrization) can make such an optimization problem tractable.

Variational Monte Carlo. Variational Monte Carlo (VMC) tackles the ground-state quantum many-body problem by optimizing the energy over a parametric class of wavefunctions. Parameter updates must be computed by sampling configurations according to the Born rule for the wavefunction. Recently, we introduced a Rayleigh-Gauss-Newton approach to VMC optimization which improves on existing methods for recently introduced neural-network-based parametrizations.

High-dimensional probability. The committor function is a fundamental object in the study of rare transitions between metastable states of a stochastic process. We recently showed that tensor networks can be used to compute committor functions in high dimensions, allowing us to examine rare transitions in a 1D Ginzburg-Landau theory.

Pictured: Mean-field dynamics for an ensemble sampler.

Monte Carlo sampling is the most flexible and widely-used tool for estimating sums and integrals in high dimensions. It plays a supporting role in Variational Monte Carlo (see High-dimensional functions above), where efficient sampling is crucial for wavefunction optimization. Conversely, parametric function classes can support the goal of Monte Carlo sampling. Some results in this area should be coming soon!

I am also interested in generic sampling problems. We introduced an ensemble MCMC sampler that can circumvent slow mixing due to metastability.

Pictured: Bold Feynman diagram expansion for the GW approximation to the Luttinger-Ward functional.

Background. Beyond the single-particle picture of density functional theory (DFT), many of the most widely used computational methods in quantum many-body physics are based on the formalism of Green's functions, which encode response and excitation properties of a system. Many-body perturbation theory (MBPT), which expands quantities of interest perturbatively in the strength of the inter-particle interaction, defines a major category of approaches to computing Green's functions. The terms in this expansion correspond to the so-called bare Feynman diagrams. These can in turn be reorganized into a series of bold Feynman diagrams. These objects can be understood in terms of a construction called the Luttinger-Ward (LW) functional. But the construction is only formal, and recently the existence of a single-valued LW functional has been cast into doubt by theoretical and numerical evidence.

Euclidean lattice field theory. We have rigorously justified the LW formalism in the context of Euclidean lattice field theory. In particular, we have rigorously justified the combinatorial arguments underlying the bold diagrammatic expansion, constructed the LW functional via a non-perturbative argument, and and proved that the bold diagrammatic expansion forms an asymptotic series for the LW functional.

DMFT. The dynamical mean-field theory (DMFT) is a quantum embedding theory in which Green's functions play a central role. See Quantum embedding above for further details on theoretical and practical work in this area.

Adaptive diagonal basis sets for electronic structure
SciCADE (July 2024)
[slides]

Direct interpolative construction of quantized tensor trains
Tensor4All Meeting (April 2024)
[slides]

Interacting ensemble MCMC and fast entropically regularized SDP
Mathematics of Data and Decisions at UC Davis (MADDD) Seminar (November 2023)
[slides]

Efficient sampling for lattice QMC
Julian Schwinger Foundation Workshop on the Fermion Sign Problem (July 2023)
[slides]

Scalable variational embedding for quantum many-body problems
SIAM Conference on Mathematical Aspects of Materials Science (May 2021)
[slides]

Optimization for variational Monte Carlo with neural quantum states
Modeling and Simulation Group Seminar: Machine Learning in Science at NYU (April 2021)
[slides]

Optimal transport via a Monge-Ampère optimization problem
SIAM Conference on the Mathematics of Data Science (May 2020)
[slides]

Toward sharp error analysis of extended Langrangian molecular dynamics for polarizable force field simulation
Ki-Net Young Researchers Workshop (October 2019)
[slides]

Semidefinite relaxation of multi-marginal optimal transport, with application to strictly correlated electrons in second quantization
ICIAM (July 2019)
[slides]

A classical statistical mechanics approach to understanding Green's function methods and the Luttinger-Ward formalism
Oberwolfach (March 2018)
[slides]

Adaptive compression for Hartree-Fock-like equations
SIAM Conference on Applied Linear Algebra (May 2018)
[slides]

UC Berkeley
Spring 2024:Math 128B
Fall 2023: Math 228A
Spring 2023: Math 128B
Fall 2022: Math 228A

New York University
Spring 2022: Linear Algebra I (graduate)
Fall 2021: Mathematical Statistics
Spring 2021: Linear Algebra I (graduate)
Fall 2020: Calculus I

UC Berkeley (GSI)
Spring 2018: Math 54, Alexander Paulin [section page]
Spring 2016: Math 53, Denis Auroux [quizzes]
Fall 2015: Math 1B, Ole Hald

Two views on optimal transport and its numerical solution (2015). My undergraduate thesis (supervised by Yanir Rubinstein and Rafe Mazzeo), which presented two new formulations of optimal transport problems leading to two corresponding methods for numerically solving them. This thesis won the Kennedy Thesis Prize for the top undergraduate thesis in the natural sciences at Stanford.
[.pdf]

Asymptotics of Hermite polynomials (2015). A largely expository paper (for a course on orthogonal polynomials) about asymptotics of Hermite polynomials and the Gaussian Unitary Ensemble (GUE). Presents a result about the stationary states for the quantum harmonic oscillator, which, though likely nothing new, I think is fairly cool.
[.pdf]

Spectral methods for neural computation (2013/14). A presentation for the Brains in Silicon lab outlining some ideas about how favorable Fourier-domain properties of certain neural tuning curves are naturally suited (in an idealized setting) for the computation of simple functions.
[slides]

3D Shape Understanding Using Machine Learning (2013). A presentation about my work on using a deep learning framework to perform labeled segmentation of discrete surfaces and extract multiscale learned shape descriptors. To help with training, I introduced a new set of shape descriptors based on conformal maps.
[slides]
(Note: research carried out during CURIS 2013 in Stanford's Geometric Computation Group.)

The k-discs algorithm and its kernelization (2012). Introduces and analyzes an extension of k-means allowing cluster centroids to be discs of arbitrary dimension, capable of recovering more diverse cluster geometries.
[.pdf]
(Note: class project for CS 229 at Stanford.)